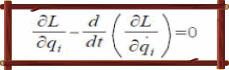�y�����E�N�O�̊w������A���N�Ԃ̉�͗͊w�̃Z�~�i�[�ɏo�Ȃ����B�e�L�X�g�͖���Goldstein�́u�ÓT�͊w�v�B�_�����x�[���̉��z�d���̌��������ʉ����W�Ƃ������̂��`���A�܂��A�k���s-�u�Ƃ���Lagrange�̕��������B���Ԃ̗��Ȃ�Newton���̂����ł͂킸��킵���������Ă�����Lagrangian���g���Ƃ��Ƃ������ɉ����邱�Ƃɂ��������������I�I�i�O�O�j
�Ƃ܂������܂ł̓t���t���Ƃ悩�����̂����A�ϕ������̂����肩�班���������Ȃ��Ă����i�O�O�j�G�B�B�B ���Ƃ́h�Ⴓ�h�Ɓh�C�́h�����ŃZ�~�i�[�ɂłĂ��������悤�ȁB�B�B ���ǁA�Z�~�i�[�͑�U�� �ϕ�������Lagrange�̕��������ꂩ���Z�� Hamilton�̉^���������Ƒ�[�͂̐����ϊ��̓r���܂łŏI������B�B�B
�܂��A���ꂩ��܂ɂӂ�Ă͉�͗͊w�̃e�L�X�g��R�Ƃ��Ă݂͂��肵�����A�����̕ό`��ǂ������Œ��g�̗������T�b�p����������A��̕�����ēz�̓i�����I �����ϊ��Ńi�����I�Ƃ���������ł����O���O�����Łi�O�O�j�G�G���̂����e�L�X�g�ɚ������Ԃ�悤�ɂȂ����B�B�B
���ꂩ��Y�`�b�g �y���`�b�g������������A�C���^�[�l�b�g���g���������̃T�C�g�i������Close�j���������B�����ł̓l�b�g�ʼn�͗͊w�̗֓ǂ����Ƃ������ƂŁA�ʂ����Č����̊w������B�ɂ��Ă����邩����Ƒ傢��畏����Ȃ�����x����Ȃ�����G���g���[���邱�Ƃɂ����B�e�L�X�g�͍��� �N�i�������̐搶�̃t�@���ł���܂��j�́u�ʎq�͊w���w�Ԃ��߂̉�͗͊w����v��������łQ�ŁB���̖{�̑��݂͏��ł̍�����m���Ă����B�����A�{���Ńp���p���ƃy�[�W���J���Ă݂����A�����I�Ȃ��Ƃ���ő債���Ȃ��Ȃ��ƁA�h�����h�Ɓh�Ό��h�ɂ��{���ɂ��Ă������i�O�O�j�G�̂����A��������ł��w�����l�b�g�̗֓ǂɂ��킹�ēǂݐi��ł����ƁA�i���ƍ��ؒ��J�ɂ킩��₷���������R���p�N�g�ɗv�̂悭�A�������I�Ȑ[���Ӗ��܂ŋL�q����Ă���Ȃ��Ƃ��炽�߂Ċ�����������ł���܂��B�i�O�O�j�G�G
�܁A�����������Ƃłӂ����щ�͗͊w�������@��Ɍb�܂ꂽ�킯�ŁA�ϔN�̋^����Ȃ�ƂȂ��������悤�ȋC�i���������킯�ł͂Ȃ��E�E�E�O�̂���)�ɂȂ��Ă����B
�����̂悤�ɉ�͗͊w���ăT�b�p������Ȃ��Ƃ��A���O���̂��I�]�}�V�C�Ƃ��v���Ă������������������Ǝv���܂����A�ȉ��̏��u���ɏ����ł������ɗ��Ă�B�B�B
1 ���z�d���̌���
2 �ϕ�������Euler-Lagrange�̕�����
3 �����^���������Ɛ����ϊ�
4 Hamilton-Jacobi�̗��_
5 Poison����
6 �ʑ����
�V Lagrangian�̑Ώ̐��ƕ�����
���z�d�����ĉ��z�̎d���̂��Ƃ��B�Ȃ�Έ�̉��̖��ɗ��H�Ƃ��l���̂��Ȃ��A���Ȃ��ł���`�I�I�����A�q���b�Ƃ��ĉ��̂��Ƃ��ȁA�܂�������(^^)�B
�����ł͗͊w�n�̒ނ荇���Ƃ������͈̂�̂Ȃɂ��A�Ƃ����悤�Ȃ��Ƃ�Nj����čŌ�ɂd���������|�k���������������̕��������o���Ƃ����������������܂��B
�������w������ɉ�͗͊w�̃Z�~�i�[�ł͂��߂ĉ��z�d���̌������K�����Ƃ��搶�i�������f���q�_���U����Ă����ƋL�����邪�j�͉��z�ψʂ̐��������̂悤�ɂȂ��ꂽ�B�u�f��̓t�B�����̃R�}����œ����Ă���悤�Ɍ����܂��ˁB�Ƃ���ł��̒�����P�R�}���o���āA�����Ɏʂ��Ă���u�c�������������Ă��B���ꂪ���z�ψʂƂ������̂ł��B�v �t�`��A����Ȃ��̂��B�Ȃ�ƂȂ����������悤�ȁA��̂̃C���[�W�����߂��悤�ȋC�������B�������A�i���ł���Ȃ�����l����Ƃ�����ɂ�`(���ق܂邾��)(^^);;�Ƃ����_�ɂ��Ă͂قƂ�ǐ[���Nj����Ȃ��������B�B�B�܂����z�d���̍l��������Euler-Lagrange�̕��������łĂ���̂ɂ͐��������Ăт����肵��(^^)�B
�ڍׂ͂����� �� ���z�d���̌����Ƃd��������-�k��������������������.pdf
�������w���R�����낾�������Ȃ��AHuckel�̕��q�O���@�Ƃ������̂��K�����B�Ȃ�ƃx���[���̃G�l���M�[���ʂ����ɊȒP�Ȍv�Z�łłĂ���̂ɂт����肵�����A�����ł͂��߂ĕϕ��@�Ƃ������̂�m�����B�܂��Ƃɂ����ϕ��}�j���A���ɏ]���Čv�Z����G�l���M�[���v�Z�ł����B
���āA�O�u�́u���z�d���̌����v�ł́A�n�̉^���̂���u�Ԃ̏�ԂƁA���̏�Ԃ���̉��z�ψʁi�������ω��j�̍l�@�|D�fAlembert�̌����|���o���_�Ƃ���Euler-Lagrange�̕����������B���̂����́A����� �h���������h ���o���_�Ƃ������̂ł���B
������� �h�ϕ������h �Ƃ����悤�Ȃ��̂���Euler-Lagrange�̕��������������̂ł͂Ȃ����ƂȂ�킯�ŁA���ꂪHamilton�̌����i�ϕ������j�Ƃ�������̂ł���B���� ��1 ���� ��2 �̊Ԃɂ킽��n�̉^���̑S�̂ɂ��āA�n�����ۂɍs�Ȃ��^�������߂�̂ɁA���̉^������̉��z�ψʓI�ȕϓ��i�ϕ��j���l���A���̕ϕ����ɒl���Ƃ�悤�ɂ���B
�ڍׂ͂����� �� �ϕ�������Euler-Lagrange�̕�����.PDF
Newton�̉^���������̂�����Euler-Lagrange�̉^���������ł��ׂĂ��Ƒ��肽�̂ł͂Ȃ����H Hamiltonian�Ƃ������̂���т����Ă������AHamiltonian��Lagrangian�͂ǂ����ǂ��������̂��I
�����ϊ����Ă����̍��W�ϊ��Ƃ��������A���炢�X�������O�����Ă���Ȃ��B����Lagrangian�͂ǂ��Ȃ�̂��B�������������e���݂����ĂĂ����̂ɁB�B�B �܂��A������Ĉ�̂Ȃɂ��̂��B�₽��ƕΔ�������łĂ��ĖڂɈ����ł͂Ȃ����B�B�B
���炢�����Ȗ��O��t���Ď��s�����Ǝv������(^^); ���ƂɈ����킯�ɂ͂����ʁB���̂܂ܐi�����B�������[���Ȃ��Ƃ�������͂����Ȃ��i�O�O�j�B
���āA��ʂɎ��R�x���̗͊w�n�́A
Lagrangian L=L(q1,q2,���qf,q1',q2',���qf'�j �@
��p���Ď���f��Euler-Lagrange�������ŋL�q�ł����B
d/dt(��L/��qi')�|��L/��q��=0 i=1,���f �A
�܂��A�l���Ă����ϐ��ϊ���
qi=qi(Q1,Q2,�E�E�E,Qf)
�̌`�̂��̂ŁA�E�ӂɂ͂p�̎��Ԕ����������Ă��Ȃ��ꍇ�ł������B�����A�E�ӂɂp�f�������Ă�����Lagrangian��ϊ�����Ƃpi,�pi',�pi''�̊��ƂȂ��āhLagrangian�͕ϐ��Ƃ�����1�K�����̊��ł���h�Ƃ����g�g�i�@���Q�Ɓj���͂ݏo���A���_���g���Ȃ��Ȃ����Ⴄ�B���̓_�����ǂ��A����ɍL���`�̕ϐ��ϊ��������悤�ɂ����̂��u�����ϊ��̗��_�v�Ƃ�����ł��ȁi�O�O�j�B���ɂ��̘b��Ɉڂ�B
���̗��_�̃~�\�́A�ϐ��̐��𑝂₵�Ď��Ԕ����̊K����������B����ƁA���̑��₵���ϐ��̊ԂŎ��Ԕ������܂܂Ȃ��ϐ��ϊ����l������Ƃ����_�ɂ���܂��B���ɊȒP�ȋ�̗�����Ă݂܂��傤�B
Newton�̉^���������͎��Ԃɂ��ĂQ�K�̔����������ƂȂ�B
md2��/dt2=F
�Ƃ���ł��̕��������ȒP�����邽�߂ɁA���ۂ̉^���ł͈ʒu���Ɖ^���ʂ��̕ω��͖��W�ł͂��肦�Ȃ����A�����ł͈ʒu���W�����^���ʂ�(=mdx/dt�j���h�ϐ��h�ƍl���Ď��Ԕ����̊K�����P�K������Ƃ������������ʂ���Ă��܂��ˁB���̌��ʁA���̕������ƂȂ�B
dp/dt=F
����قǎ��Ԃ̂P�K�����������ƂȂ����B����Ƃ����ƕ��G�ȗ͊w�n�ɂ�����Ɠ���������K�p�ł��Ȃ����ƂȂ��Ă��܂��ˁB���̂��߂ɂ́A��ʉ����W�Ƃ���ʉ��^���ʂƂ��Ă悤�ɁA�܂��^���ʂƂ����T�O��Newton���̎��ʁ~���x�Ƃ�����`����g������K�v������B�����ĐV������`�����^���ʂ��h�Ɨ��ϐ��Ƃ݂Ȃ��h���Ƃɂ��܂��B��̓I�ɐV�����^���ʂ������Ē�`����B
pi�߁�L/��qi�f
�����œV����I�ł��邪�AHamiltonian��o�ꂳ����B(^^);
Hamiltonian�������Œ�`����B
H = ��piqi'-L
�����^����������
qi'= ��H(q;p)/��pi
pi'= -��H(q;p)/��qi i=1,���,f
�ƂȂ�܂��B���̎��͕ϐ� pi �𑝂₵�������Ɏ��Ԕ����̊K���������邱�Ƃ��ł���(^^)�B
�ڍׂ͂����� �� �����`���̗��_.PDF
�����ϊ��Ƃ͈�ʂɐ����^�������������藧�V�����ϐ��̑gQ��,�o���ւ̕ϊ��ł���ƒ�`����܂��B�܂萳���ϊ����Hamiltonian��K�Ƃ����
qi'= ��H(q;p)/��pi �����ϊ� Qi'= ��K(Q;P)/��Pi
pi'= -��H(q;p)/��qi �� Pi'= -��K(Q;P)/��Qi
�����ϊ��͕���i�v�j�Ƃ������̂Ŋ��S�ɋK�肳��܂��B������ăi�����Ƃ������Ƃɂ��Ắu�����ϊ��ƕ��.pdf�v�����Ă��������Ƃ��āA�����ł͓V����I�Ɂi�O�O�j�G�����W�Ƃ���ƁA�����ϐ��͕�����玟���ɂ���ē������Ƃ������Ƃ�m���Ă����悢�ł��傤�B
[����] �@�`�C�̕��W�͂��ꂼ��Ɨ��ϐ��̈قȂ�������ŁA�����ē�������ł͂���܂����`�I�i�ڂ����́u�����ϊ��ƕ��.pdf���Q�Ɓv�j�B
�@ pi= ��W/��qi, Pi=-��W/��Qi, K=H+��W/��t
�A qi=-��W/��pi, Pi=-��W/��Qi, K=H+��W/��t
�B pi= ��W/��qi, Qi= ��W/��Pi, K=H+��W/��t
�C qi=-��W/��pi, Qi= ��W/��Pi, K=H+��W/��t
�Ƃ������ƂłP��̓I�ȗ�������Č��܂��B
�y���z
�������W(x,y)����~�����W�n(r,��)�ւ̕���ɂ�鐳���ϊ������߂�B
�y���z
x=rcos��, y=rsin�ӂƏ����܂��ˁB�A�̊W�����g���B���W��px,py�ł̔����� x, y ���o�Ă���悤��W�Ƃ���
W=-px�rcos��-py�rsin��
�Ƃ���悢���Ƃ��킩��܂��B����ƇA�����
Px=-��W/��r, Py=-��W/�݃�
�ƂȂ�܂����琳���ϊ���̐V�����^����P�͎����ŗ^�����܂��B
Px=pxcos��+pysin��, Py=-pxrsin��+pyrcos�� //
�ڍׂ͂����� �� �����ϊ��ƕ��.PDF
�ϊ��̒��ł�pi=Pi�AQi=qi�Ƃ����ϊ��͉����ϊ����Ă��Ȃ��ϊ��ŁA������P���ϊ��Ƃ����܂��B�Ƃ���ōP���ϊ�����ق�̏����������ꂽ�ϊ������ϊ��Ƃ����܂��B�������ϊ��͐����ϊ��ł���̂ŁA�������ϊ��̕�������݂��܂��B�����ŁA�u���W�̖��������i�i��Ԑ��i�j�v�u��������]�v�u���Ԑ��i�v�̖������ϊ����l����ƁA���ꂼ��̕ϊ��ݏo����������݂���킯�ŁA���̕���͎��͂����Ƌ������̂������Ƃ������ƂɂȂ�܂��B
�����ł͌��ʂ����������Ă����܂��B�ڂ����́u�������ϊ�.pdf�v���Q�Ƃ��Ă��������B
X��V�������W�n�ł̈ʒu�x�N�g���A���������W�n�ł̈ʒu�x�N�g���Ƃ��܂��A�Â͖������������������x�N�g���Ƃ��܂��B����ƍ��W�̖��������i�͎����ŗ^�����܂��ˁB
X�����{��
���̂悤�Ɋe���W���͕��s�����A���_�����ꂽ�V�������W�n�ŕ����n���L�q���������Ƃ��A��Ԑ��i�Ƃ����܂��B
�����W�n�ŁA���q�̑��x�͓����ł�����^���ʂ������ł��ˁB�����Ŗ������ω��͎����ŏ������Ƃ��ł��܂��B
��xi��Xi-xi=��i
��pi��Pi-pi=0 i=1,2,3
��������A���̏d�v�Ȍ��_�������邱�ƂɂȂ�܂��B
��Ԑ��i�̕���͖{���I�ɉ^���ʂł����B
x-y���W�n�������Ƃ�����]����X-Y���W�n�ŋL�q�����ʒu�x�N�g��������(X,Y)�Ƃ����
X=xcos��+��sin��
Y=-xsin��+ycos��
�ƂȂ�܂��ˁB���A�p�Ƃ��������ł���Ƃ��A������ÂƏ����ƁA��������]�͎����ŗ^�����܂��B
��x��X-x=��y
��y��Y-y=-��x
�܂��Ax��y�����̉^���ʂ����l�ɂ��Ď����ŗ^���邱�Ƃ��ł��܂��B
��px=m(X'-x')=��py
��py=m(Y'-y')=-��px
��������A���̏d�v�Ȍ��_�������邱�ƂɂȂ�܂��B
��������]�̕���͊p�^���ʂł���B
�������̐����ϐ���qi(t)��pi(t)�Ƃ��܂��B���̂Ƃ��A�������Â������ꂽ���W�n�ɂ����āA����炪���ꂼ��Qi(T),Pi(T)�ł���Ƃ����
Qi(T)=qi(t)
Pi(T)=pi(t)
�����藧���܂��B������ T=t+�ÂƂ���B
��������A���̏d�v�Ȍ��_�������邱�ƂɂȂ�܂��B
���������Ԑ��i�̕����Hamiltonian�ł���B
�����Ƃ������Č����ƁA
���ԊԊu dt �̊Ԃ̌n�̉^����Hamiltonian�����Ƃ��閳�����ϊ��ɂ���ċL�q�ł���
�Ƃ������ƂɂȂ�܂��B
�ڍׂ͂����� �� �����ϊ��Ɩ������ϊ�.pdf
Hamilton-Jacobi�̕������Ƃ����A�݂̂��i�ǂƂ͂���Ȃ��j�V�����[�f�C���K�[�̔g���͊w�_���I�W�̒��ŁA�ނ��͂��߂ėʎq�͊w�̔g�����������o������P�_���ɍڂ��Ă����Ȃ��i�_���I�W�j�B�܂����̍����I�ȓ������͗y���ɏ����̗����������̂ł��������A
��S/�݂��{H�i���G��S/�݂�,���j���O
�Ƃ����悤�ȕ��������ڂ��Ă������Ƃ��A�s�v�c�Ƃ��܂ł������Ă���B�������̎p���X�b�L���Ƃ��Ă��Ă��������悩�������炩���m��ʁB�������AS�Ƃ͈�̂ȂƂ������Ƃ������Ɏv�������Ƃ��v���o���B
Hamilton-Jacobi�̕������Ƃ͈�̃i�����Ƃ������ƂɂȂ�킯�ł����A���̑O�������ϊ��ƕ���̍����ēǂ��Ă������Ƃ����X�X�����܂��B
���āAHamilton-Jacobi�̕������Ƃ���̂ȂƂ�����قǂ̖���ɖ߂�܂����A��������܂������ϊ����l���ĉ^�����������y�ɉ����悤�ɂ��邽�߂̏���Ⳃł���B�B�B�Ə����͍l���Ă���܂��B
���̈�[����̓I�ȗ�Ō��Ă݂܂��傤�B
�y��z
���ʂP�A�p�U�����ւ̂P�������a�U���q���l����BHamiltonian��
H=��/2�(p2+q2)
�ƂȂ�܂��B���̒��a�U���q�̉^�������A����ԁi�ʑ���ԁj��ŕ`���ƁA�p���x�ւ̔����v���̓����~�^���ƂȂ�܂��ˁB�܂莿�_�͔��a��i�QE/��)�̉~������v���Ɉ�葬�x�ŃN���N������Ă��邱�ƂɂȂ�B�����ŁA�p���x�ւʼn�]���Ă����]���W�n�ɏ��ڂ�Ǝ��_�͎~�܂��Č����邱�ƂɂȂ�܂��ˁB�܂��A�����Ă݂���̂悤�ȍ��W�ϊ��������ꍇ�̕�������Hamilton-Jacobi�̕��������Ə����͗������Ă��܂��B
���āA���A�����ʂɐ����Ȏ��̉��̊p���x�ւ̉�]���W��Q,P�Ƃ����
����Qcos��t�{Psin��t �� Q����cos�ւ��|��sin�ւ�
����Pcos�ւ��|Qsin�ւ� �� P����cos�ւ��{��sin�ւ�
�ƂȂ�B���̕ϊ���^���鐳���ϊ��̕��W�́i�V����I�ł��邪(^^);;�j
W(���CQ�C��)���i���Qcos�ւ��|�Q��Q�{Q�Qcos�ւ��j/�Qsin�ւ�
�{���ɂ��ꂪ���߂����ł��邩�A�ȉ��Ɍ�����ƁA����͂�,Q,t�̊��ł��邩��A�����ϊ��ƕ���̍����Q�l�ɂ���
������W/�݂� ���Q����cos�ւ��|��sin�ւ�
P���|��W/��Q��肑��P�������ւ��{�pcos�ւ�
��������B���ꂩ�炱�̕���͐���������ł��邱�Ƃ��킩�����B���āA�ϊ����Hamiltonian��K�Ƃ���� K��H�{��W/�݂� �ƂȂ�B��W/��t���v�Z�����
��W/�݂����|��/2�iP�Q�{Q�Q�j
������Ƃ�Hamiltonian��
H����/�Q�i���Q�{���Q�j����/�Q�iP�Q�{Q�Q�j
�]���ĕϊ����Hamiltonian K�̓[���ƂȂ�B������������
Q�f����K/��P���O�A P�f���|��K/��Q���O
�ƂȂ�A���ꂩ�� Q���萔�AP=�萔�Ƃ������ʂ�������B�܂��]���W�nP-Q�ł͒��a�U���q�̎��_�́u�Î~�v�𑱂���Ƃ������ƂɂȂ�킯�ł��ˁB
�O�U��͂��̂��炢�ɂ��āA�ڍׂ͎��̃��|�[�g���Q�Ƃ��Ă��������B
�ڍׂ͂����� �� Hamilton-Jacobi�̗��_.pdf
�ʎq�͊w�ł��Ȃ��݂̌����W�́A�ÓT�͊w��Poisson���ʂ���̗ސ����瓱���ꂽ�i�f�B���b�N�ʎq�͊w������4��P�P�P�R�j�B
�����ł́APoisson���ʂ̐�����Poisson���ʂƐ����������Ƃ̊W�A�܂��A�������ϊ��Ƃ̊W�ȂǂׂĂ݂܂��傤�B
���ׂ͂����� �� Poisson����.pdf
�w�����A������I����Ń��O�����W�A���Ƃ������̂��������ˁB �k���s�|�u�Ƃ����āA�s�͉^���G�l���M�[�A�u�̓|�e���V�����G�l���M�[���B
���ꂳ����������Ƃ͊ȒP�B�d��������-�k���������������̕������������A���߂�͊w�n�̉^�����|�|���|���Əo�Ă���B����Ńo���U�`�C�A�o���U�`�C���c�����Ƃ��낾���B�B�B�V�J�V�˃F�A������A���̒������Â��͂Ȃ���l�F�B�B�B
�Ⴆ�A1�����̗͂̓����Ă��Ȃ����R���q���l���Ă݂悤�B���̏ꍇ�A�|�e���V�����͂O�ł��邩��A��̏���Ⳃɂ��������Ăk��������������������
�k���i�P�^�Q�j�����f�O�Q
���Ƃ���������B���̂k�������������������͂d���������|�k���������������̎����m���Ɏ��R���q�̉^��������
�i�����h���O�j��^����B����������ň��S���Ă͂����Ȃ���A������B
�k�������������������Ƃ���
�k���������i�����f�j
�Ƃ����z���l���Ă��A�d���������|�k���������������̎���莩�R���q�̉^����������^����B�܂��A����������Ă���Ă݂Ă������������B�ڂ����̓e�L�X�g�o�S�S�ɍڂ��Ă���ˁB�B�B�����������Ȃ�ƁA�k���s�|�u�Ƌ��ȋʏ��̂悤�Ɋo���Ă��������i�H�j�͐r���S���ƂȂ��Ȃ��Ă���B���ǁA�k�������������������́u�B��ł͂Ȃ��i�k�������������������̑��l���j�v�Ƃ����B�B�B�т����肷�鎖�����������X�̎����ƂȂ��Ă����̂�������A�o�o���o���o���B
������ǂ����邩�B�����œo�ꂷ��̂����̗L���Ȃm�������������̍P�����Ȃ̂ł���B���̍P�����̂������ŗL�ۖ��ۂ̂k�������������������̒�����^�̎��R���ۂ��L�q����k��������������������I�яo�����Ƃ��ł���悤�ɂȂ����̂��B
�����A�����A������A������A�����Ȃ��ŁA�����Ȃ��ŁA�܂��܂��Ȃ͋Ă����B�I�b�A�����̂�����A������Ń��]���]���Ă��Ȃ��œ������������I�x�Ƃ����А��̂����Ăт��݂̐��Ńn�b�g�ڂ��o�܂��܂����B���̏�ɂ̓e�L�X�g�V�� �k�������������������̑Ώ̐��ƕ����ʂ̒�`���J����Ă��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�ڍׂ͂����� �� �m�������������̍P����.pdf
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@